Case Study: Hacker Statistics¶
This chapter will allow you to apply all the concepts you’ve learned in this course. You will use hacker statistics to calculate your chances of winning a bet. Use random number generators, loops, and Matplotlib to gain a competitive edge!
Random float¶
Randomness has many uses in science, art, statistics, cryptography, gaming, gambling, and other fields. You’re going to use randomness to simulate a game.
All the functionality you need is contained in the random package, a sub-package of numpy. In this exercise, you’ll be using two functions from this package:
seed(): sets the random seed, so that your results are reproducible between simulations. As an argument, it takes an integer of your choosing. If you call the function, no output will be generated.rand(): if you don’t specify any arguments, it generates a random float between zero and one.
import numpy as np
# Set the seed
np.random.seed(123)
# Generate and print random float
print(np.random.rand())
0.6964691855978616
Roll the dice¶
In the previous exercise, you used rand(), that generates a random float between 0 and 1.
As Hugo explained in the video you can just as well use randint(), also a function of the random package, to generate integers randomly. The following call generates the integer 4, 5, 6 or 7 randomly. 8 is not included.
import numpy as np
np.random.randint(4, 8)NumPy has already been imported as np and a seed has been set. Can you roll some dice?
# Print randint() to simulate a dice
print(np.random.randint(1,7))
# Use randint() again
print(np.random.randint(1,7))
3 5
Determine your next move¶
In the Empire State Building bet, your next move depends on the number of eyes you throw with the dice. We can perfectly code this with an if-elif-else construct!
The sample code assumes that you’re currently at step 50. Can you fill in the missing pieces to finish the script? numpy is already imported as np and the seed has been set to 123, so you don’t have to worry about that anymore.
# Starting step
step = 50
# Roll the dice
dice = np.random.randint(1,7)
# Finish the control construct
if dice <= 2 :
step = step - 1
elif dice <= 5 :
step = step + 1
else :
step = step + np.random.randint(1,7)
# Print out dice and step
print(dice)
print(step)
3 51
The next step¶
Before, you have already written Python code that determines the next step based on the previous step. Now it’s time to put this code inside a for loop so that we can simulate a random walk.
# NumPy is imported, seed is set
# Initialize random_walk
random_walk = [0]
# Complete the for loop
for x in range(100) :
# Set step: last element in random_walk
step = random_walk[-1]
# Roll the dice
dice = np.random.randint(1,7)
# Determine next step
if dice <= 2:
step = step - 1
elif dice <= 5:
step = step + 1
else:
step = step + np.random.randint(1,7)
# append next_step to random_walk
random_walk.append(step)
# Print random_walk
print(random_walk)
[0, -1, 0, 1, 2, 1, 0, -1, -2, -3, -4, -5, -6, -5, 0, -1, -2, -1, -2, -1, 0, 1, 2, 3, 2, 3, 2, 3, 4, 5, 6, 5, 9, 10, 9, 10, 9, 10, 11, 12, 13, 14, 15, 16, 19, 20, 21, 22, 27, 28, 32, 33, 32, 33, 34, 33, 34, 35, 37, 38, 39, 38, 37, 38, 39, 38, 37, 38, 39, 41, 40, 39, 40, 39, 40, 41, 42, 44, 43, 44, 45, 46, 47, 48, 47, 46, 47, 46, 47, 48, 47, 50, 51, 52, 53, 52, 53, 54, 58, 57, 56]
How low can you go?¶
Things are shaping up nicely! You already have code that calculates your location in the Empire State Building after 100 dice throws. However, there’s something we haven’t thought about – you can’t go below 0!
A typical way to solve problems like this is by using max(). If you pass max() two arguments, the biggest one gets returned. For example, to make sure that a variable x never goes below 10 when you decrease it, you can use:
x = max(10, x - 1)# Initialize random_walk
random_walk = [0]
for x in range(100) :
step = random_walk[-1]
dice = np.random.randint(1,7)
if dice <= 2:
# Replace below: use max to make sure step can't go below 0
step = max(0, step - 1)
elif dice <= 5:
step = step + 1
else:
step = step + np.random.randint(1,7)
random_walk.append(step)
print(random_walk)
[0, 2, 1, 2, 4, 5, 6, 11, 10, 11, 12, 13, 14, 15, 14, 19, 20, 21, 22, 21, 20, 19, 18, 17, 18, 19, 20, 26, 25, 24, 23, 24, 25, 26, 25, 26, 27, 26, 31, 32, 31, 30, 29, 28, 29, 28, 27, 29, 30, 33, 34, 36, 37, 38, 39, 38, 37, 38, 39, 40, 41, 40, 41, 42, 43, 46, 47, 48, 47, 48, 47, 48, 49, 50, 54, 53, 52, 53, 54, 55, 54, 55, 54, 55, 57, 62, 61, 62, 63, 64, 65, 66, 67, 66, 67, 68, 69, 71, 73, 72, 73]
Visualize the walk¶
Let’s visualize this random walk! Remember how you could use matplotlib to build a line plot?
import matplotlib.pyplot as plt
plt.plot(x, y)
plt.show()The first list you pass is mapped onto the x axis and the second list is mapped onto the y axis.
If you pass only one argument, Python will know what to do and will use the index of the list to map onto the x axis, and the values in the list onto the y axis.
# Initialization
random_walk = [0]
for x in range(100) :
step = random_walk[-1]
dice = np.random.randint(1,7)
if dice <= 2:
step = max(0, step - 1)
elif dice <= 5:
step = step + 1
else:
step = step + np.random.randint(1,7)
random_walk.append(step)
import matplotlib.pyplot as plt
# Plot random_walk
plt.plot(random_walk)
# Show the plot
plt.title('Initial Random Walk')
plt.show()
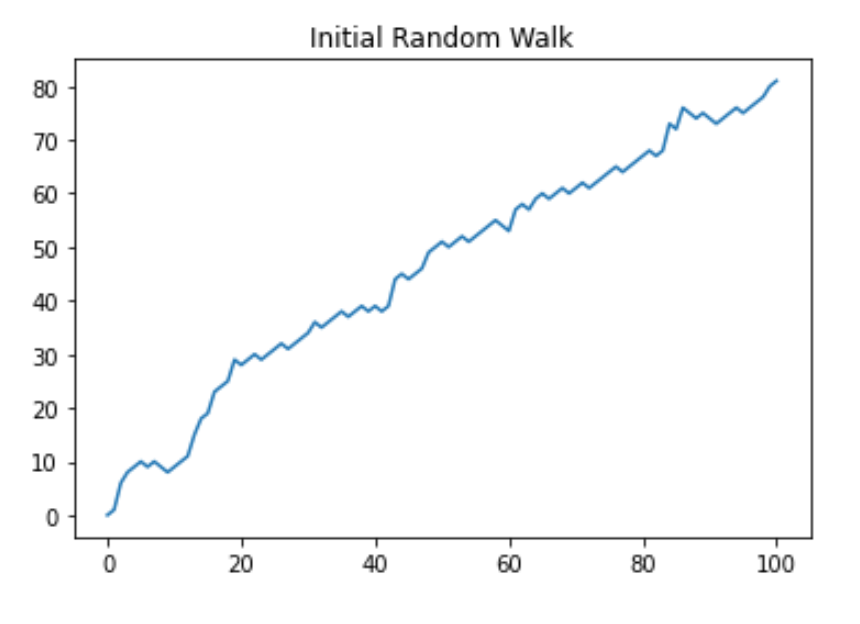
Simulate multiple walks¶
A single random walk is one thing, but that doesn’t tell you if you have a good chance at winning the bet.
To get an idea about how big your chances are of reaching 60 steps, you can repeatedly simulate the random walk and collect the results. That’s exactly what you’ll do in this exercise.
The sample code already sets you off in the right direction. Another for loop is wrapped around the code you already wrote. It’s up to you to add some bits and pieces to make sure all of the results are recorded correctly.
Note: Don’t change anything about the initialization of all_walks that is given. Setting any number inside the list will cause the exercise to crash!¶
# Initialize all_walks (don't change this line)
all_walks = []
# Simulate random walk 10 times
for i in range(10) :
# Code from before
random_walk = [0]
for x in range(100) :
step = random_walk[-1]
dice = np.random.randint(1,7)
if dice <= 2:
step = max(0, step - 1)
elif dice <= 5:
step = step + 1
else:
step = step + np.random.randint(1,7)
random_walk.append(step)
# Append random_walk to all_walks
all_walks.append(random_walk)
# Print all_walks
print(all_walks)
[[0, 0, 0, 6, 5, 6, 7, 8, 12, 13, 15, 16, 17, 18, 17, 18, 17, 18, 17, 16, 17, 16, 22, 23, 24, 26, 25, 26, 25, 26, 27, 29, 28, 32, 31, 32, 33, 34, 33, 34, 33, 32, 31, 30, 31, 32, 36, 37, 38, 37, 38, 39, 38, 39, 40, 41, 42, 46, 52, 53, 54, 55, 56, 57, 58, 59, 58, 57, 58, 59, 60, 59, 60, 59, 60, 61, 62, 63, 64, 65, 66, 67, 66, 65, 66, 67, 68, 69, 72, 73, 72, 73, 74, 75, 76, 75, 76, 77, 76, 75, 74], [0, 0, 1, 2, 1, 2, 3, 2, 1, 0, 1, 2, 3, 4, 3, 4, 5, 6, 5, 6, 5, 6, 11, 12, 13, 14, 15, 20, 19, 20, 19, 23, 24, 25, 26, 31, 35, 40, 41, 45, 44, 45, 44, 45, 44, 45, 44, 45, 46, 45, 44, 43, 44, 45, 44, 50, 49, 48, 49, 48, 49, 55, 56, 55, 56, 57, 58, 57, 56, 62, 63, 64, 65, 66, 67, 71, 72, 73, 75, 74, 75, 76, 75, 76, 77, 78, 79, 78, 77, 78, 79, 78, 79, 80, 81, 80, 82, 83, 82, 88, 87], [0, 2, 1, 0, 1, 0, 1, 0, 1, 2, 3, 2, 7, 8, 9, 10, 9, 8, 9, 12, 13, 16, 17, 16, 17, 16, 15, 21, 20, 21, 22, 23, 24, 23, 25, 24, 23, 24, 25, 24, 23, 22, 21, 20, 21, 22, 23, 22, 23, 28, 27, 28, 29, 30, 31, 30, 29, 30, 31, 30, 31, 30, 32, 33, 38, 40, 39, 40, 41, 42, 43, 42, 41, 45, 46, 47, 46, 45, 44, 43, 44, 45, 44, 43, 42, 48, 49, 48, 47, 48, 47, 51, 50, 51, 52, 53, 52, 53, 52, 53, 54], [0, 0, 0, 0, 1, 2, 3, 4, 3, 2, 3, 2, 1, 0, 1, 2, 1, 5, 4, 3, 4, 3, 2, 3, 4, 5, 8, 9, 8, 14, 15, 21, 22, 23, 22, 23, 24, 25, 30, 29, 30, 31, 32, 31, 32, 33, 34, 33, 32, 33, 34, 33, 32, 31, 33, 34, 33, 34, 40, 41, 42, 43, 44, 45, 46, 47, 48, 54, 55, 56, 55, 54, 55, 56, 55, 56, 55, 56, 57, 58, 60, 61, 62, 63, 64, 63, 64, 63, 64, 67, 68, 69, 72, 73, 74, 75, 76, 77, 76, 77, 78], [0, 1, 3, 2, 3, 2, 1, 2, 3, 7, 6, 7, 13, 14, 15, 14, 15, 16, 17, 18, 19, 20, 19, 18, 19, 20, 19, 18, 19, 18, 19, 20, 19, 20, 21, 22, 28, 29, 30, 31, 30, 35, 34, 35, 40, 41, 42, 41, 42, 43, 42, 45, 49, 50, 56, 61, 62, 64, 63, 64, 65, 66, 65, 66, 65, 66, 65, 66, 65, 64, 65, 66, 65, 66, 65, 66, 65, 66, 67, 68, 67, 68, 67, 66, 67, 66, 67, 68, 69, 70, 71, 72, 78, 77, 78, 77, 82, 83, 82, 83, 84], [0, 1, 2, 3, 2, 3, 2, 3, 4, 5, 6, 7, 6, 7, 11, 12, 13, 12, 11, 12, 11, 12, 13, 19, 20, 23, 24, 23, 24, 25, 26, 27, 26, 27, 29, 30, 31, 32, 33, 34, 35, 34, 33, 37, 38, 37, 38, 37, 41, 42, 41, 40, 41, 42, 41, 42, 43, 45, 46, 49, 48, 49, 50, 51, 52, 53, 54, 53, 52, 53, 54, 55, 57, 58, 57, 56, 57, 56, 57, 58, 64, 63, 64, 65, 66, 67, 68, 69, 71, 70, 69, 68, 69, 70, 71, 70, 69, 70, 71, 70, 71], [0, 4, 8, 9, 11, 10, 11, 10, 11, 13, 12, 11, 10, 9, 8, 10, 11, 12, 13, 14, 18, 17, 18, 19, 20, 21, 22, 26, 27, 28, 34, 35, 34, 35, 37, 38, 44, 49, 50, 53, 52, 55, 57, 56, 57, 56, 57, 60, 63, 62, 63, 62, 63, 67, 66, 67, 68, 69, 70, 71, 70, 74, 75, 74, 79, 80, 81, 82, 87, 88, 87, 86, 87, 86, 87, 86, 87, 88, 87, 86, 87, 86, 87, 92, 93, 98, 99, 100, 99, 98, 99, 100, 99, 98, 97, 98, 97, 99, 100, 101, 100], [0, 0, 1, 2, 3, 4, 3, 4, 7, 8, 9, 10, 9, 13, 14, 19, 18, 19, 23, 22, 24, 30, 31, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 44, 45, 46, 45, 44, 46, 48, 47, 48, 47, 53, 54, 60, 61, 60, 59, 62, 63, 64, 63, 64, 65, 70, 69, 71, 70, 72, 71, 72, 73, 74, 75, 76, 77, 76, 77, 76, 82, 81, 80, 82, 83, 84, 83, 84, 85, 84, 85, 86, 87, 88, 89, 88, 89, 90, 91, 90, 89, 88, 89, 90, 92, 93, 94, 95, 94, 93, 94], [0, 1, 2, 3, 4, 5, 7, 6, 9, 10, 9, 10, 11, 14, 15, 20, 19, 25, 26, 27, 26, 25, 26, 27, 28, 29, 28, 27, 29, 30, 33, 34, 33, 32, 33, 32, 33, 32, 31, 30, 31, 30, 31, 32, 33, 32, 38, 39, 38, 39, 38, 37, 38, 39, 40, 41, 40, 41, 42, 43, 47, 48, 49, 50, 51, 50, 51, 52, 53, 52, 53, 54, 55, 59, 58, 59, 60, 61, 62, 63, 64, 65, 64, 65, 66, 67, 66, 67, 68, 67, 68, 67, 66, 67, 66, 67, 68, 69, 75, 76, 78], [0, 1, 0, 1, 0, 3, 4, 3, 4, 3, 2, 3, 4, 5, 10, 12, 13, 18, 19, 20, 24, 25, 26, 32, 33, 34, 35, 34, 35, 36, 40, 41, 42, 43, 44, 45, 46, 45, 46, 47, 46, 45, 46, 45, 46, 47, 46, 45, 46, 47, 46, 47, 48, 47, 46, 47, 46, 47, 48, 49, 48, 50, 51, 52, 51, 52, 57, 58, 57, 59, 58, 59, 60, 63, 64, 63, 62, 63, 62, 63, 64, 65, 68, 69, 68, 69, 70, 69, 70, 69, 68, 67, 68, 67, 68, 71, 72, 73, 74, 78, 80]]
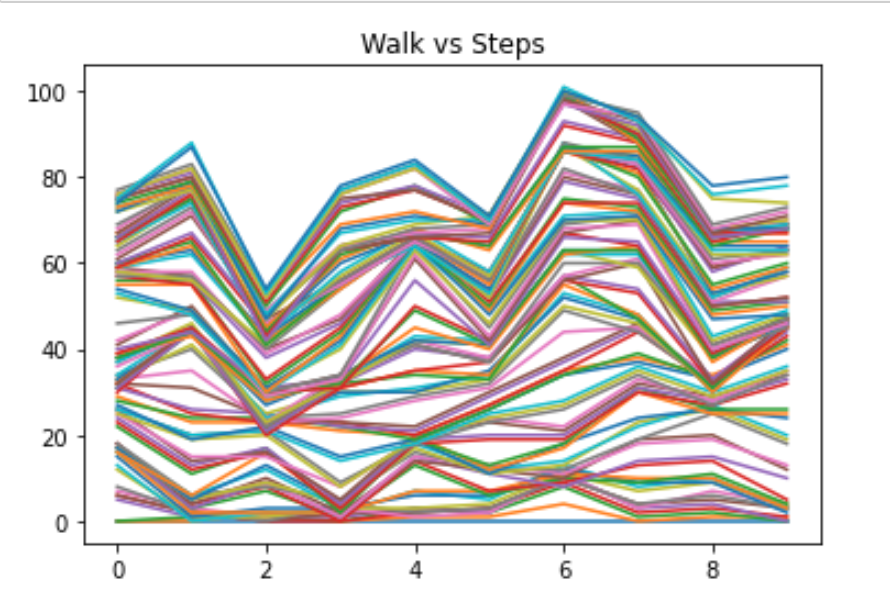
Visualize all walks¶
all_walks is a list of lists: every sub-list represents a single random walk. If you convert this list of lists to a NumPy array, you can start making interesting plots! matplotlib.pyplot is already imported as plt.
The nested for loop is already coded for you – don’t worry about it. For now, focus on the code that comes after this for loop.
# Convert all_walks to NumPy array: np_aw
np_aw = np.array(all_walks)
# Plot np_aw and show
plt.plot(np_aw)
plt.title('Walk vs Steps')
plt.show()
# Clear the figure
plt.clf()
# Transpose np_aw: np_aw_t
# Now every row in np_all_walks represents the position after 1 throw for the five random walks.
np_aw_t = np.transpose(np_aw)
# Plot np_aw_t and show
plt.plot(np_aw_t)
plt.title('Throws vs. Steps')
plt.show()
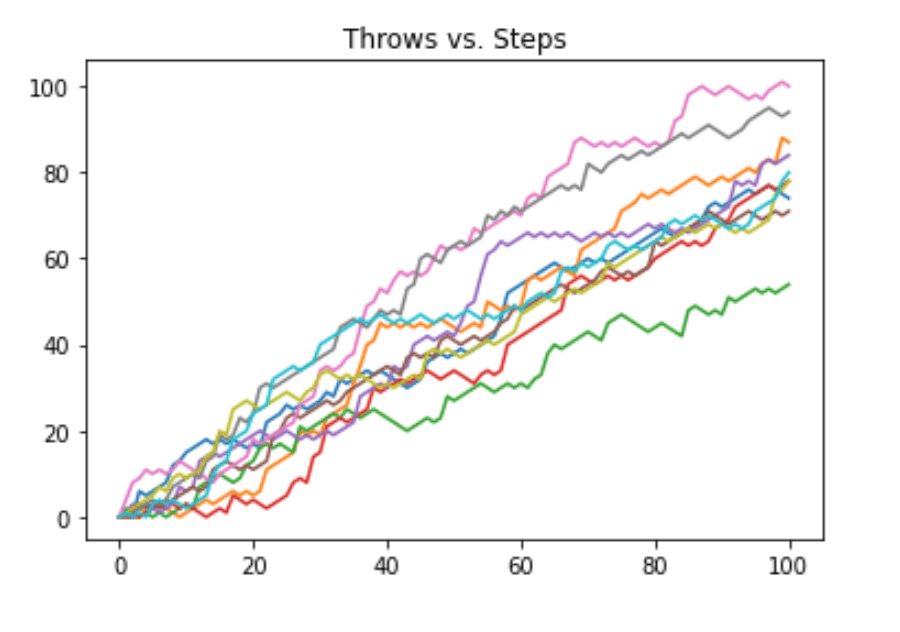
Implement clumsiness¶
With this neatly written code of yours, changing the number of times the random walk should be simulated is super-easy. You simply update the range() function in the top-level for loop.
There’s still something we forgot! You’re a bit clumsy and you have a 0.1% chance of falling down. That calls for another random number generation. Basically, you can generate a random float between 0 and 1. If this value is less than or equal to 0.001, you should reset step to 0.
# numpy and matplotlib imported, seed set
# Simulate random walk 250 times
all_walks = []
for i in range(250) :
random_walk = [0]
for x in range(100) :
step = random_walk[-1]
dice = np.random.randint(1,7)
if dice <= 2:
step = max(0, step - 1)
elif dice <= 5:
step = step + 1
else:
step = step + np.random.randint(1,7)
# Implement clumsiness
if np.random.rand() <= 0.001 :
step = 0
random_walk.append(step)
all_walks.append(random_walk)
# Create and plot np_aw_t
np_aw_t = np.transpose(np.array(all_walks))
plt.plot(np_aw_t)
plt.title('Throws vs Steps')
plt.show()
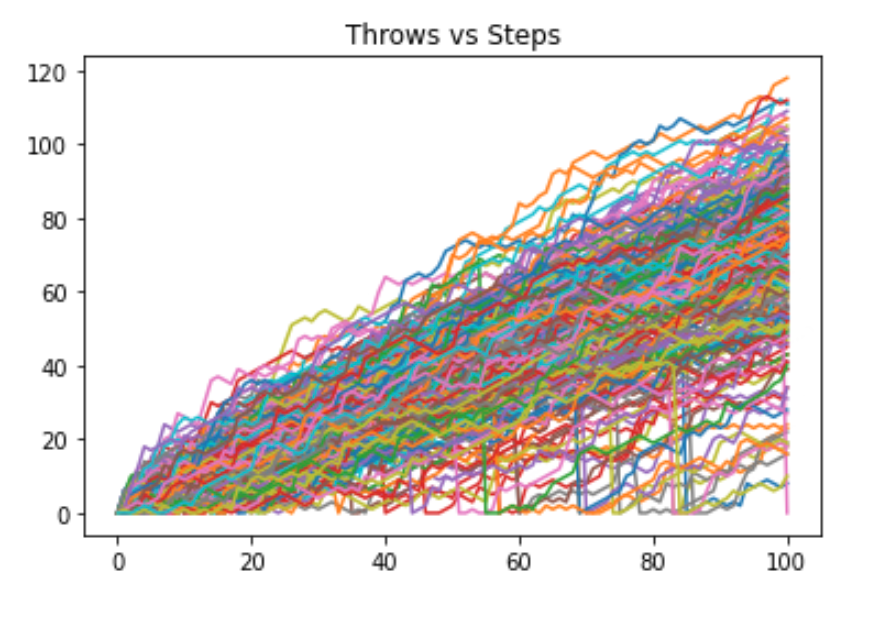
Plot the distribution¶
All these fancy visualizations have put us on a sidetrack. We still have to solve the million-dollar problem: What are the odds that you’ll reach 60 steps high on the Empire State Building?
Basically, you want to know about the end points of all the random walks you’ve simulated. These end points have a certain distribution that you can visualize with a histogram.
Note that if your code is taking too long to run, you might be plotting a histogram of the wrong data!
# Select last row from np_aw_t: ends
ends = np_aw_t[-1,:]
# Plot histogram of ends, display plot
plt.hist(ends)
plt.title('End Points of Random Walks')
plt.show()

Calculate the odds¶
The histogram of the previous exercise was created from a NumPy array ends, that contains 500 integers. Each integer represents the end point of a random walk. To calculate the chance that this end point is greater than or equal to 60, you can count the number of integers in ends that are greater than or equal to 60 and divide that number by 500, the total number of simulations.
Well then, what’s the estimated chance that you’ll reach at least 60 steps high if you play this Empire State Building game? The ends array is everything you need; it’s available in your Python session so you can make calculations in the IPython Shell.
print(np.count_nonzero(ends[ends >= 60])/np.count_nonzero(ends))
0.7349397590361446